1. 问题

为了更好的理解分析这个世界，我们习惯把现实问题建模为数学问题。比如我们把简谐运动的某个特性模拟为正玄/余玄函数：

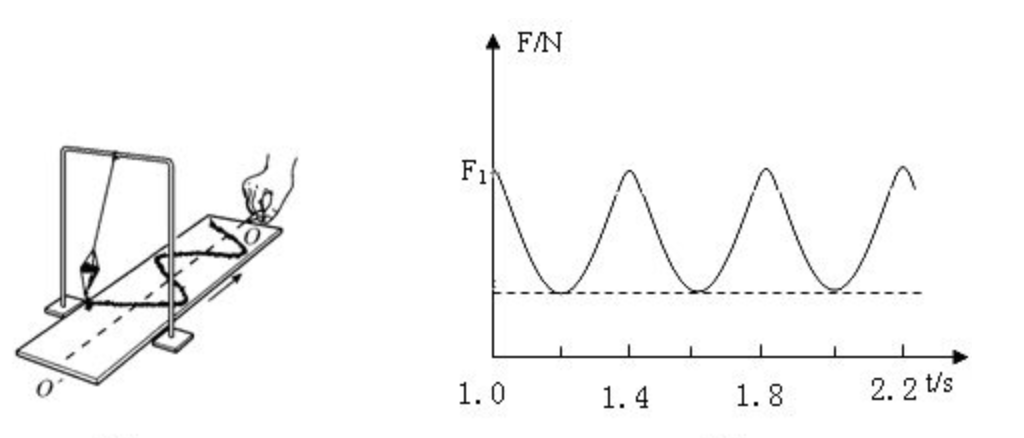
然而，现实是非常复杂的，能用函数模拟的事物是有限的，即使能用函数模拟，大部分情况也是非常复杂的函数，当前人类的数学能力不能很完美的去处理这些复杂的数学公式。

2. 局部模拟

面对复杂的函数，硬上是肯定不行的，俗话说“退一步海阔天空”，于是我们想：我们可以只研究我们关心的函数特性，或者这我们只关注函数的一部分。 假设，对于余玄函数：

我们只关心其在(x=0)附近的性质，我们可以尝试用多项式来替代(x=0)附近的(y=cos(x))。

多项式（Polynomial）是由称为不定元的变量和称为系数的常数通过有限次加减法、乘法以及自然数幂次的乘方运算得到的代数表达式。

我们先试一下一次多项式，设一次多项式：

为了让(f(x))在(x=0)附近接近(C(x)), 我们令:

$f(0) = a = C(0) = cos(0) = 1 \tag{3}$ $f^{'}(0) = b = C^{'}(0) = -sin(0) = 0 \tag{4}$

所以：

如图2.1所示，(f(x))在(x=0)附近对C(x)拟合的效果很一般。

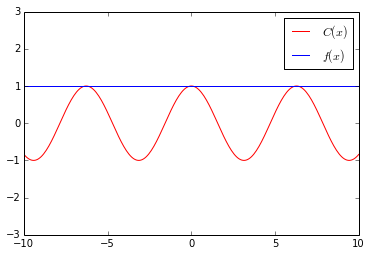
我们再来试一下二次多项式，设二次多项式：

为了让(f(x))在(x=0)附近接近(C(x)), 我们令:

$f(0) = a = C(0) = cos(0) = 1 \tag{7}$ $f^{'}(0) = b = C^{'}(0) = -sin(0) = 0 \tag{8}$ $f^{''}(0) = 2c = C^{''}(0) = -cos(0) = -1\tag{9}$

所以：

如图2-2所示，(f(x))在(x=0)附近对C(x)拟合有了很大的进步。

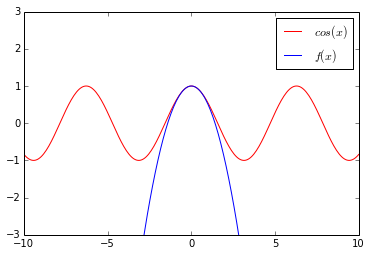
3. 泰勒展开

接下来我们来试下n次多项式，设n次多项式：

$f(x)(的k次导数为：

所以：

又因为：

根据等式(13)(14)得：

然后我们重写等式(11):

等式(16)即为(C(x)=cos(x))在0处的(2n)或(2n+1)阶泰勒展开。 随着n的增大，(f(x))对(C(x))的拟合越来越好,如图2-3与图2-4所示：

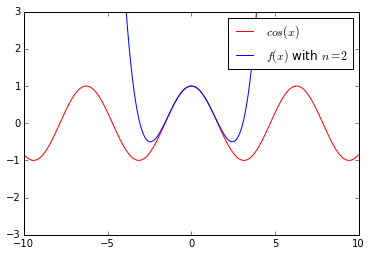
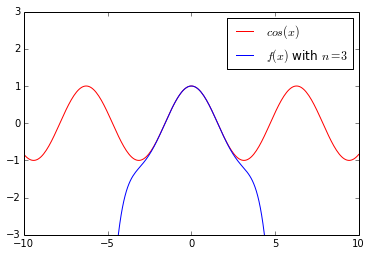
根据上述计算方式，如果函数(h(x))在某点存在n阶导数，我们可以计算出该函数在该点的n阶泰勒展开。

转载请注明出处